データの分布の可視化#
データの分析またはモデリングを行う際の最初のステップは、変数がどのように分布しているかを理解することです。分布の可視化手法は、多くの重要な質問に対する迅速な回答を提供できます。観測値の範囲は?中心傾向は?一方向に大きく歪んでいるか?双峰性の兆候はあるか?有意な外れ値はあるか?これらの質問に対する回答は、他の変数によって定義されたサブセットによって異なるか?
分布モジュール には、このような質問に答えるために設計された関数がいくつか含まれています。軸レベルの関数は histplot()、kdeplot()、ecdfplot()、および rugplot() です。これらは、図レベルの displot()、jointplot()、および pairplot() 関数内でグループ化されています。
分布を可視化するにはいくつかの異なるアプローチがあり、それぞれに相対的な長所と短所があります。特定の目的に最適なアプローチを選択できるように、これらの要素を理解することが重要です。
単変量ヒストグラムのプロット#
分布を可視化する最も一般的なアプローチはおそらく *ヒストグラム* です。これは、histplot() と同じ基盤となるコードを使用する displot() のデフォルトのアプローチです。ヒストグラムは、データ変数を表す軸が一連の離散ビンに分割され、各ビンに該当する観測値の数が対応するバーの高さを使用して示される棒グラフです。
penguins = sns.load_dataset("penguins")
sns.displot(penguins, x="flipper_length_mm")
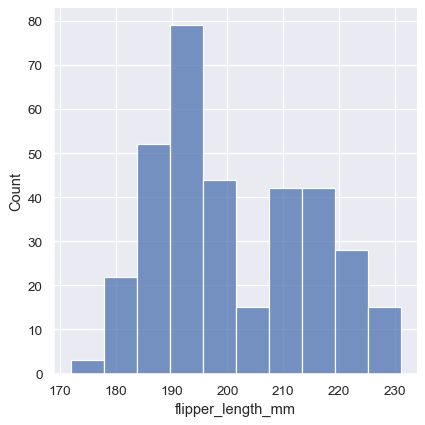
このプロットから、flipper_length_mm 変数についていくつかの洞察がすぐに得られます。たとえば、最も一般的なフリッパーの長さは約195 mmですが、分布は双峰性に見えるため、この1つの数値はデータをうまく表していません。
ビンサイズ(階級幅)の選択#
ビンのサイズは重要なパラメータであり、間違ったビンサイズを使用すると、データの重要な特徴を覆い隠したり、ランダムな変動から見かけの特徴を作成したりすることにより、誤解を招く可能性があります。デフォルトでは、displot()/histplot() は、データの分散と観測値の数に基づいてデフォルトのビンサイズを選択します。ただし、このような自動的なアプローチに過度に依存するべきではありません。なぜなら、それらはデータの構造に関する特定の仮定に依存しているからです。分布の印象が異なるビンサイズで一貫していることを常に確認することをお勧めします。サイズを直接選択するには、binwidth パラメータを設定します。
sns.displot(penguins, x="flipper_length_mm", binwidth=3)
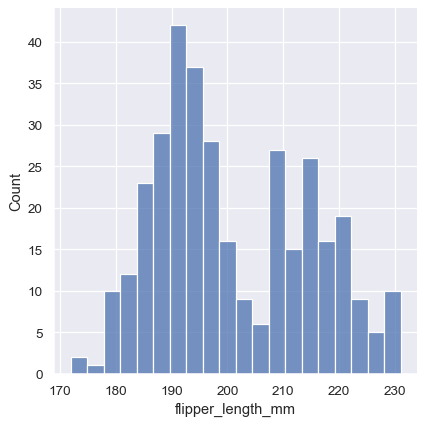
他の状況では、ビンの *数* を指定する方が、サイズを指定するよりも理にかなっている場合があります。
sns.displot(penguins, x="flipper_length_mm", bins=20)
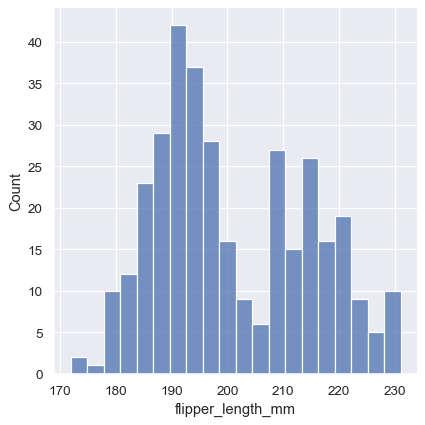
デフォルトが失敗する状況の1つの例は、変数が比較的小さい数の整数値をとる場合です。その場合、デフォルトのビン幅が小さすぎて、分布に不自然なギャップが生じる可能性があります。
tips = sns.load_dataset("tips")
sns.displot(tips, x="size")
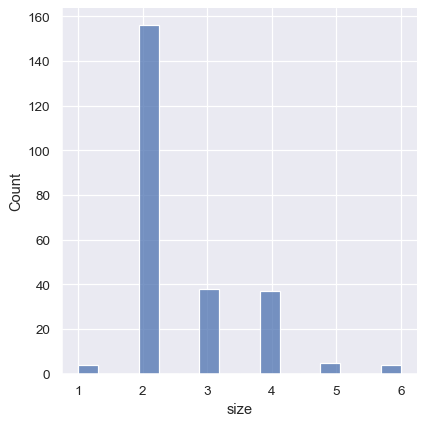
1つのアプローチは、配列を bins に渡すことによって、正確なビンの区切りを指定することです。
sns.displot(tips, x="size", bins=[1, 2, 3, 4, 5, 6, 7])
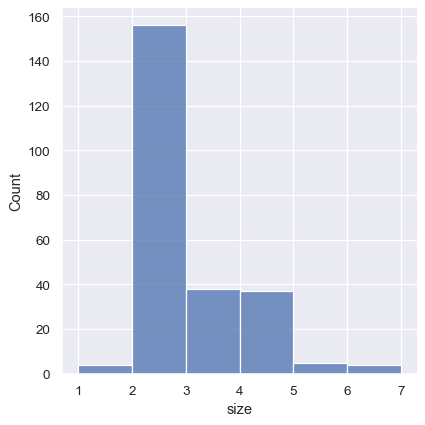
これは、discrete=True を設定することによっても実現できます。これは、対応する値を中心とするバーを持つデータセットの一意の値を表すビンの区切りを選択します。
sns.displot(tips, x="size", discrete=True)
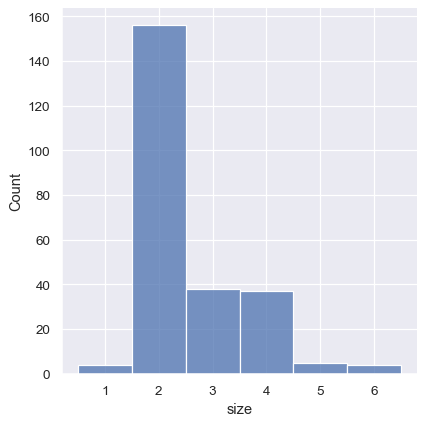
ヒストグラムのロジックを使用して、カテゴリ変数の分布を可視化することもできます。離散ビンはカテゴリ変数に自動的に設定されますが、軸のカテゴリ的性質を強調するためにバーをわずかに「縮小」することも役立つ場合があります。
sns.displot(tips, x="day", shrink=.8)
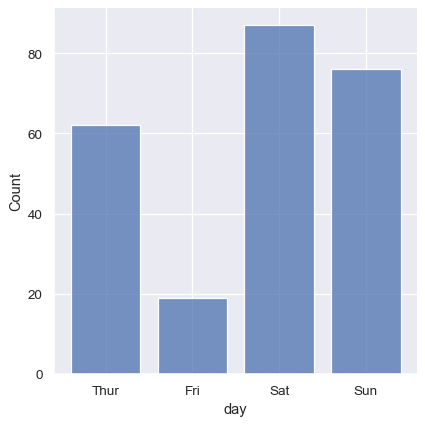
他の変数による条件付け#
変数の分布を理解したら、次のステップは、多くの場合、その分布の特徴がデータセット内の他の変数によって異なるかどうかを尋ねることです。たとえば、上記のフリッパーの長さの双峰性分布の原因は何でしょうか? displot() および histplot() は、hue セマンティクスを介した条件付きサブセット化をサポートしています。変数を hue に割り当てると、その一意の値ごとに個別のヒストグラムが描画され、色で区別されます。
sns.displot(penguins, x="flipper_length_mm", hue="species")
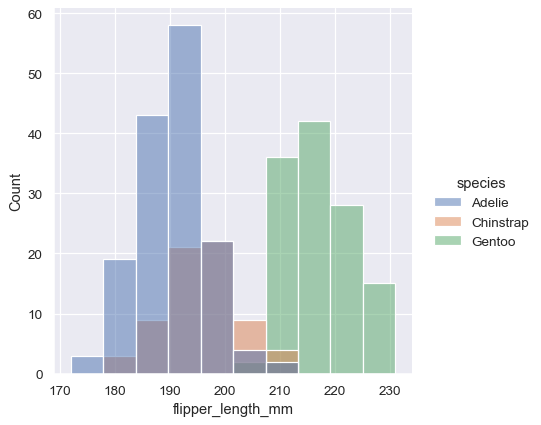
デフォルトでは、異なるヒストグラムは互いに「重ね」られており、場合によっては区別が難しい場合があります。1つのオプションは、ヒストグラムの視覚的表現を棒グラフから「ステップ」プロットに変更することです。
sns.displot(penguins, x="flipper_length_mm", hue="species", element="step")
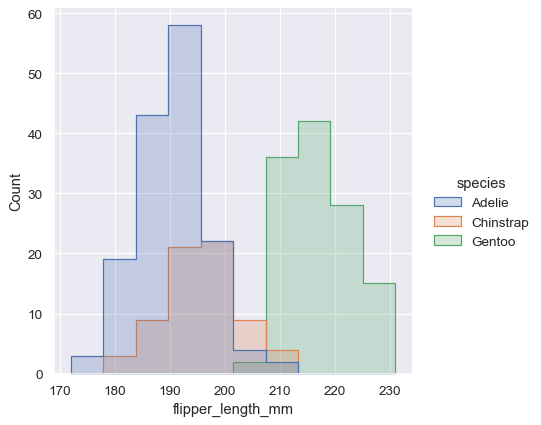
あるいは、各バーを重ねる代わりに、「積み重ねる」か、垂直に移動することができます。このプロットでは、完全なヒストグラムのアウトラインは、単一の変数のみのプロットと一致します。
sns.displot(penguins, x="flipper_length_mm", hue="species", multiple="stack")
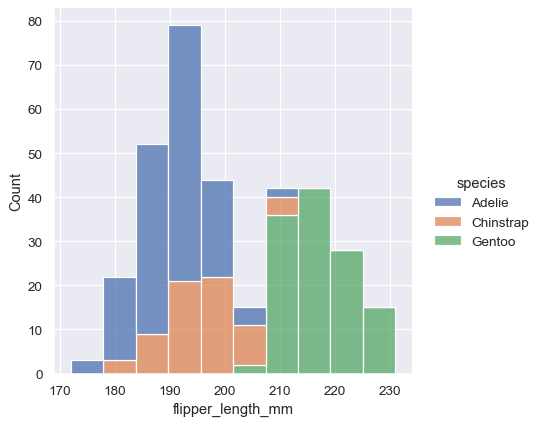
積み上げヒストグラムは、変数間の部分と全体の関係を強調しますが、他の特徴を覆い隠す可能性があります(たとえば、アデリー分布のモードを決定することは困難です)。別のオプションは、バーを「回避」することです。これは、バーを水平に移動して幅を狭くします。これにより、重複がなくなり、バーの高さが比較可能になります。ただし、カテゴリ変数のレベル数が少ない場合にのみうまく機能します。
sns.displot(penguins, x="flipper_length_mm", hue="sex", multiple="dodge")
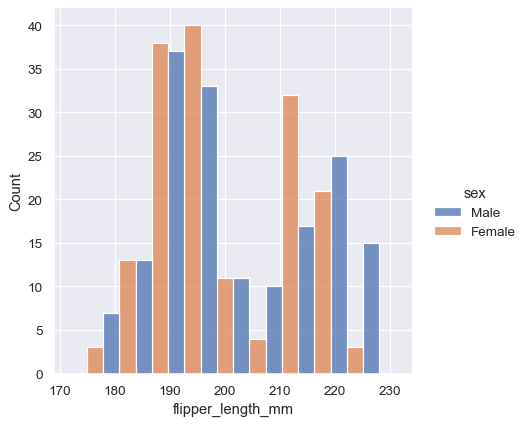
displot() は図レベルの関数であり、FacetGrid 上に描画されるため、2番目の変数を hue ではなく(またはに加えて)col または row に割り当てることにより、個々の分布を個別のサブプロットに描画することもできます。これは各サブセットの分布をよく表していますが、直接比較するのが難しくなります。
sns.displot(penguins, x="flipper_length_mm", col="sex")
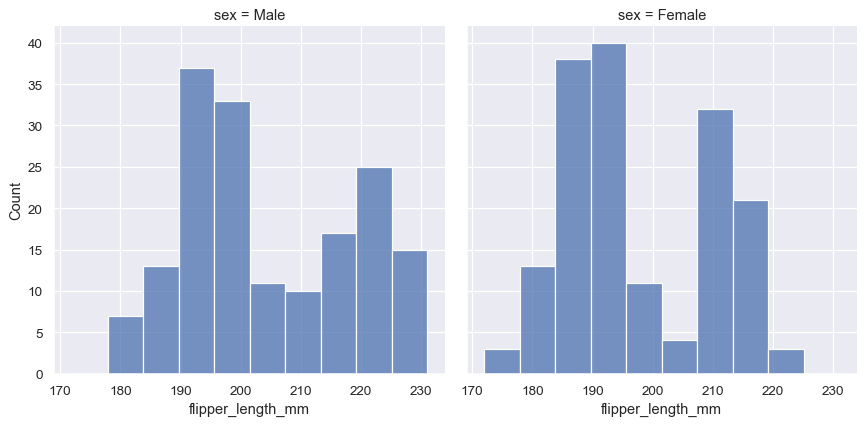
これらのアプローチはどれも完璧ではなく、すぐに比較タスクにより適したヒストグラムの代替手段をいくつか紹介します。
正規化されたヒストグラム統計#
その前に、もう1つ注意すべき点は、サブセットの観測値の数が等しくない場合、カウントの観点から分布を比較することは理想的ではない場合があるということです。1つの解決策は、stat パラメータを使用してカウントを *正規化* することです。
sns.displot(penguins, x="flipper_length_mm", hue="species", stat="density")
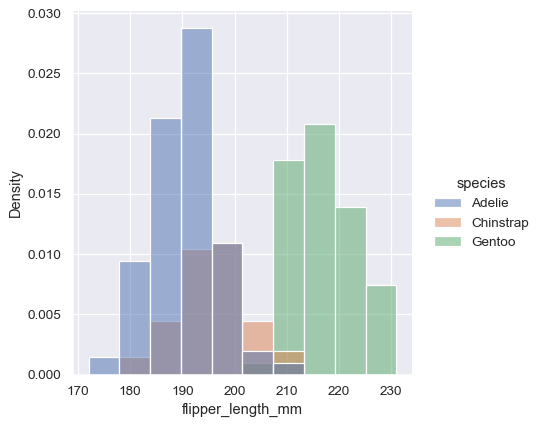
ただし、デフォルトでは、正規化は分布全体に適用されるため、これは単にバーの高さを再スケーリングするだけです。common_norm=False を設定することにより、各サブセットは個別に正規化されます。
sns.displot(penguins, x="flipper_length_mm", hue="species", stat="density", common_norm=False)
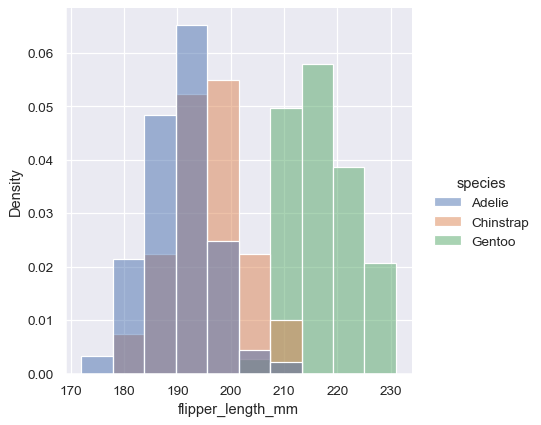
密度正規化は、*面積* の合計が1になるようにバーをスケーリングします。その結果、密度軸は直接解釈できません。別のオプションは、*高さ* の合計が1になるようにバーを正規化することです。これは、変数が離散的な場合に最も理にかなっていますが、すべてのヒストグラムのオプションです。
sns.displot(penguins, x="flipper_length_mm", hue="species", stat="probability")
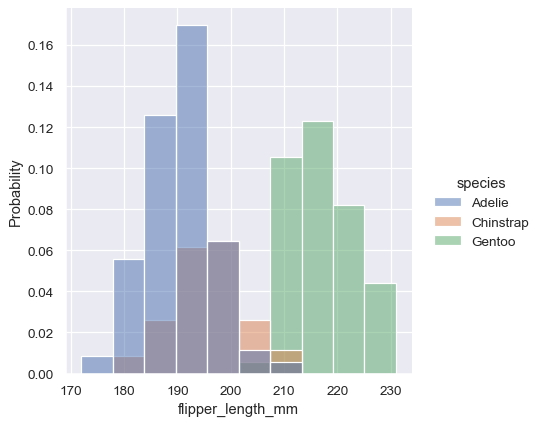
カーネル密度推定#
ヒストグラムは、観測値をビン化してカウントすることにより、データを生成した基になる確率密度関数を近似することを目的としています。カーネル密度推定(KDE)は、同じ問題に対する異なる解決策を提示します。離散ビンを使用する代わりに、KDEプロットはガウスカーネルで観測値を平滑化し、連続密度推定を生成します。
sns.displot(penguins, x="flipper_length_mm", kind="kde")
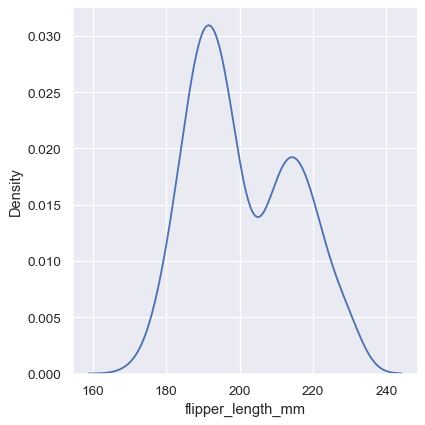
平滑化バンド幅の選択#
ヒストグラムのビンサイズと同様に、KDEがデータを正確に表す能力は、平滑化バンド幅の選択に依存します。過度に平滑化された推定値は意味のある特徴を消去する可能性がありますが、過度に平滑化されていない推定値はランダムノイズ内の真の形状を覆い隠す可能性があります。推定値のロバスト性をチェックする最も簡単な方法は、デフォルトのバンド幅を調整することです。
sns.displot(penguins, x="flipper_length_mm", kind="kde", bw_adjust=.25)
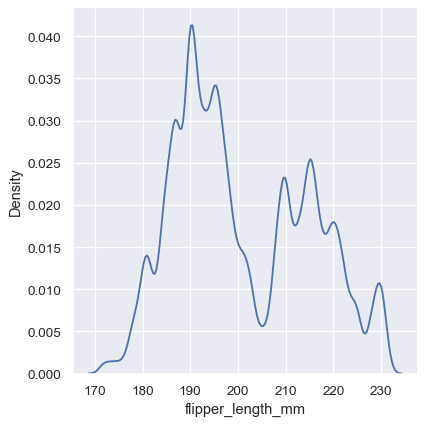
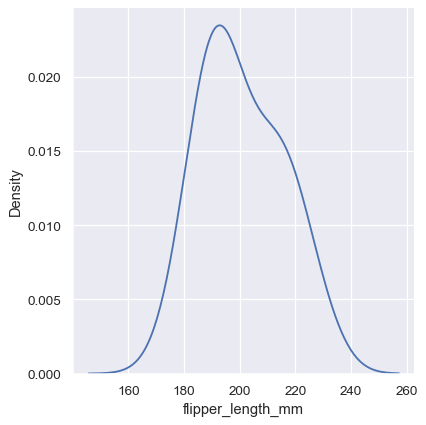
狭いバンド幅は双峰性をはるかに明らかになりますが、曲線ははるかに滑らかではありません。対照的に、広いバンド幅は双峰性をほぼ完全に覆い隠します。
sns.displot(penguins, x="flipper_length_mm", kind="kde", bw_adjust=2)
他の変数による条件付け#
ヒストグラムと同様に、hue 変数を割り当てると、その変数の各レベルに対して個別の密度推定値が計算されます。
sns.displot(penguins, x="flipper_length_mm", hue="species", kind="kde")
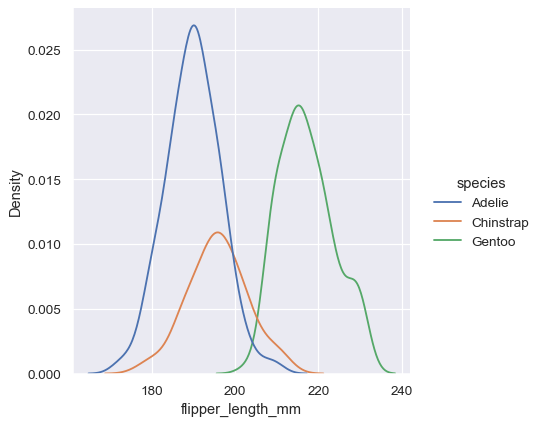
多くの場合、重ねられたKDEは重ねられたヒストグラムよりも解釈しやすいので、比較タスクに適しています。ただし、複数の分布を解決するための同じオプションの多くは、KDEにも適用されます。
sns.displot(penguins, x="flipper_length_mm", hue="species", kind="kde", multiple="stack")
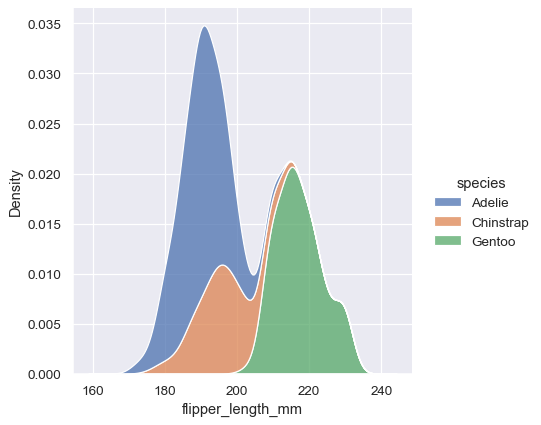
積み重ねられたプロットは、デフォルトで各曲線の間の領域を塗りつぶしていることに注意してください。個々の密度を解決しやすいように、デフォルトのアルファ値(不透明度)は異なりますが、単一または重ねられた密度の曲線を塗りつぶすこともできます。
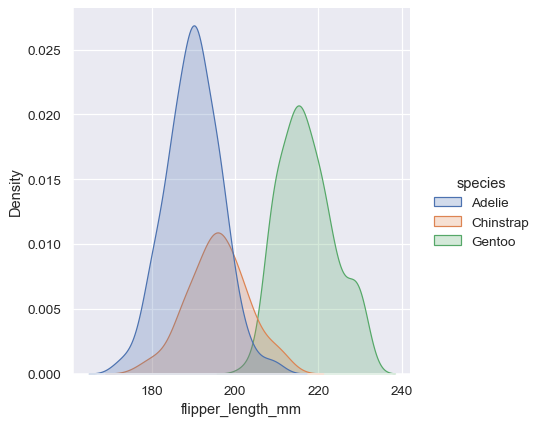
sns.displot(penguins, x="flipper_length_mm", hue="species", kind="kde", fill=True)
カーネル密度推定の落とし穴#
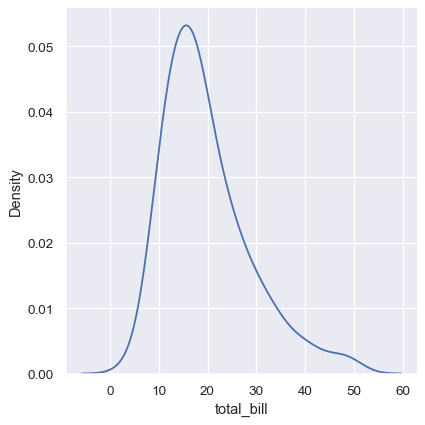
KDEプロットには多くの利点があります。データの重要な特徴(中心傾向、双峰性、歪度)を容易に識別でき、サブセット間の比較も容易です。しかし、KDEが基礎となるデータを適切に表現できない状況もあります。これは、KDEのロジックが、基礎となる分布が滑らかで境界がないことを前提としているためです。この仮定が失敗する原因の1つは、変数が本質的に境界のある量を反映している場合です。境界近くに観測値がある場合(たとえば、負にならない変数の値が小さい場合)、KDE曲線が非現実的な値にまで拡張される可能性があります。
sns.displot(tips, x="total_bill", kind="kde")
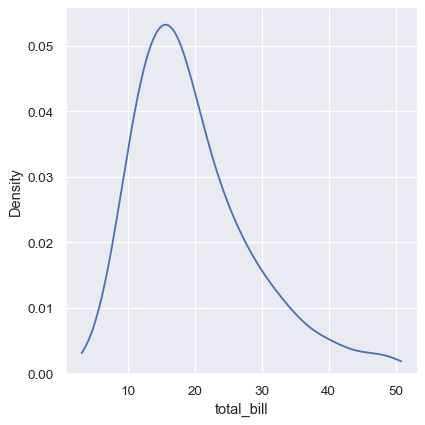
これは、cutパラメータを使用することで部分的に回避できます。このパラメータは、曲線が極値データポイントを超えてどの程度拡張されるかを指定します。ただし、これは曲線が描画される場所のみに影響します。密度推定は、データが存在できない範囲でも平滑化されるため、分布の極値で人工的に低くなります。
sns.displot(tips, x="total_bill", kind="kde", cut=0)
KDEアプローチは、離散データの場合、またはデータが本質的に連続しているが特定の値が過剰に表現されている場合にも失敗します。覚えておくべき重要なことは、KDEは、データ自体が滑らかでない場合でも、*常に滑らかな曲線を表示する*ということです。たとえば、このダイヤモンドの重量の分布を考えてみましょう。
diamonds = sns.load_dataset("diamonds")
sns.displot(diamonds, x="carat", kind="kde")
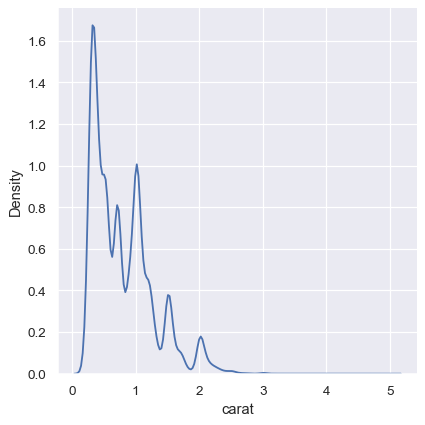
KDEは特定の値の周りにピークがあることを示唆していますが、ヒストグラムははるかにギザギザの分布を明らかにしています。
sns.displot(diamonds, x="carat")
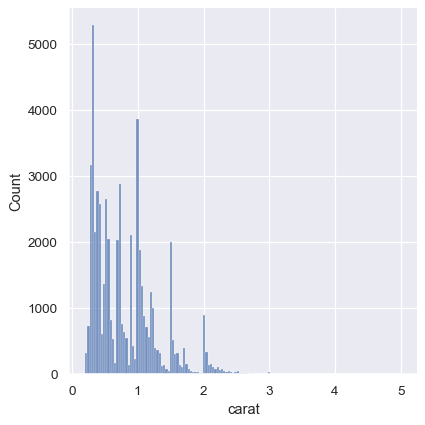
妥協案として、これら2つのアプローチを組み合わせることが可能です。ヒストグラムモードでは、displot()(histplot()と同様に)には、平滑化されたKDE曲線を含めるオプションがあります(kind="kde"ではなく、kde=Trueに注意してください)。
sns.displot(diamonds, x="carat", kde=True)
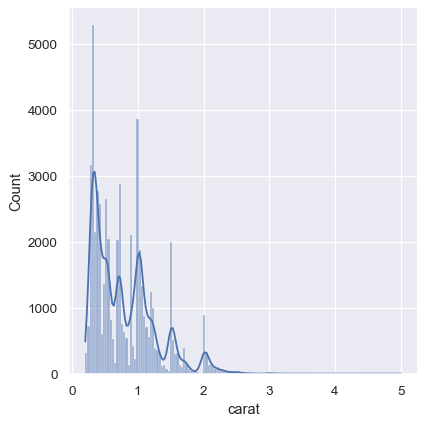
経験累積分布#
分布を視覚化する3番目のオプションは、「経験累積分布関数」(ECDF)を計算することです。このプロットは、各データポイントを単調増加する曲線で描き、曲線の高さが、より小さい値を持つ観測値の割合を反映するようにします。
sns.displot(penguins, x="flipper_length_mm", kind="ecdf")
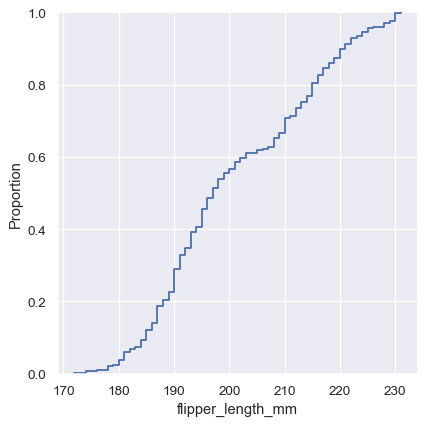
ECDFプロットには、2つの重要な利点があります。ヒストグラムやKDEとは異なり、各データポイントを直接表します。つまり、考慮すべきビンサイズや平滑化パラメータはありません。さらに、曲線が単調増加しているため、複数の分布を比較するのに適しています。
sns.displot(penguins, x="flipper_length_mm", hue="species", kind="ecdf")
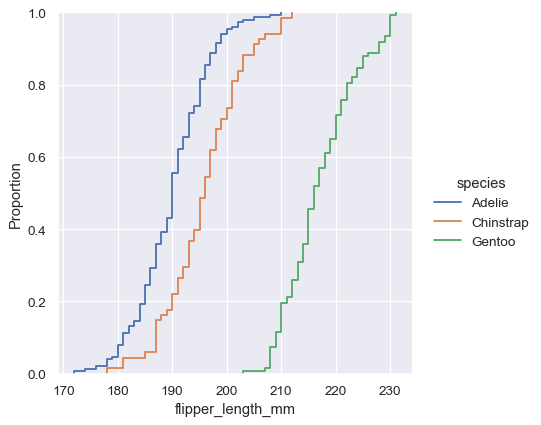
ECDFプロットの主な欠点は、ヒストグラムや密度曲線よりも分布の形状を直感的に表現しないことです。ヒストグラムではフリッパーの長さの双峰性がすぐにわかりますが、ECDFプロットで見るには、さまざまな傾きを探す必要があります。それでも、練習すれば、ECDFを調べて分布に関するすべての重要な質問に答えることができるようになり、これは強力なアプローチになる可能性があります。
二変量分布の視覚化#
これまでのすべての例では、*単変量*分布、つまり単一変数の分布(おそらくhueに割り当てられた2番目の変数で条件付けられている)を検討しました。ただし、2番目の変数をyに割り当てると、*二変量*分布がプロットされます。
sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm")
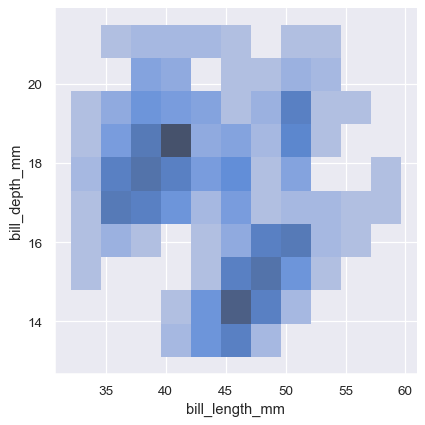
二変量ヒストグラムは、プロットをタイル状に並べた長方形内にデータをビン分割し、塗りつぶしの色で各長方形内の観測値の数を示します(heatmap()と同様)。同様に、二変量KDEプロットは、(x、y)観測値を2Dガウスで平滑化します。デフォルトの表現では、2D密度の*等高線*が表示されます。
sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", kind="kde")
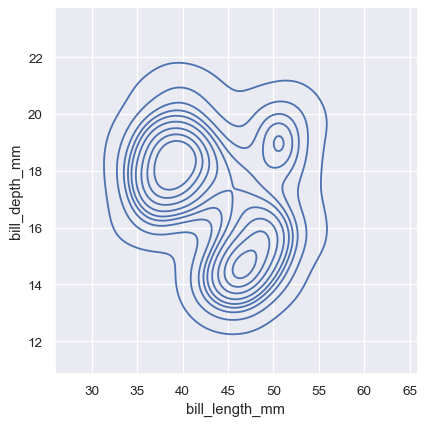
hue変数を割り当てると、異なる色を使用して複数のヒートマップまたは等高線セットがプロットされます。二変量ヒストグラムの場合、これは、条件付き分布間の重複が最小限の場合にのみうまく機能します。
sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", hue="species")
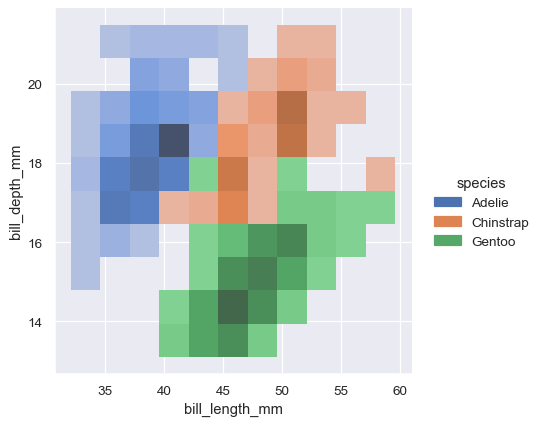
二変量KDEプロットの等高線アプローチは、重複の評価により適していますが、等高線が多すぎるプロットは煩雑になる可能性があります。
sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", hue="species", kind="kde")
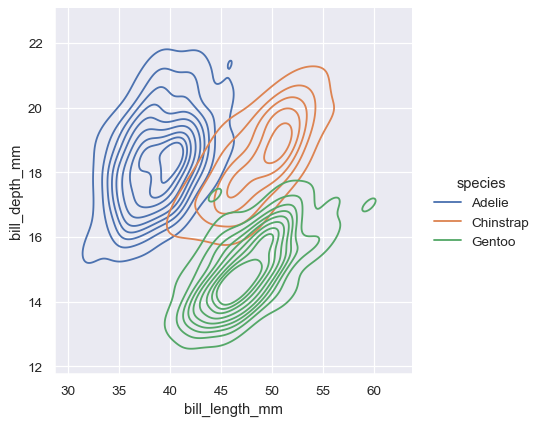
単変量プロットと同様に、ビンサイズまたは平滑化帯域幅の選択によって、プロットが基礎となる二変量分布をどの程度適切に表すかが決まります。同じパラメータが適用されますが、値のペアを渡すことで、各変数に対して調整できます。
sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", binwidth=(2, .5))
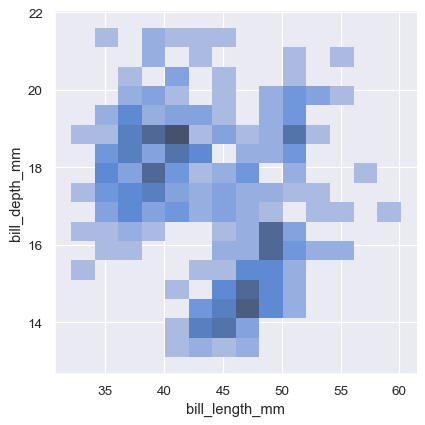
ヒートマップの解釈を助けるために、カラーバーを追加して、カウントと色の強度間のマッピングを表示します。
sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", binwidth=(2, .5), cbar=True)
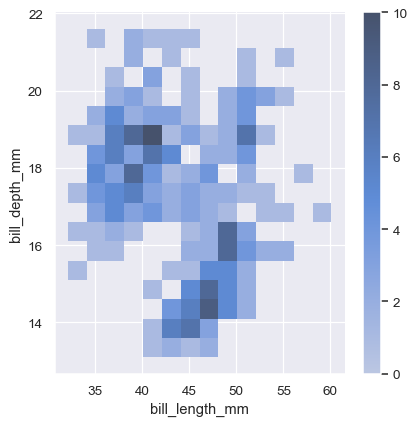
二変量密度等高線の意味はそれほど単純ではありません。密度は直接解釈できないため、等高線は密度の*等比率*で描画されます。つまり、各曲線は、密度の一部*p*がその下にあるようなレベルセットを示します。threshパラメータによって制御される最低レベルと、levelsによって制御される数で、*p*値は均等に配置されます。
sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", kind="kde", thresh=.2, levels=4)
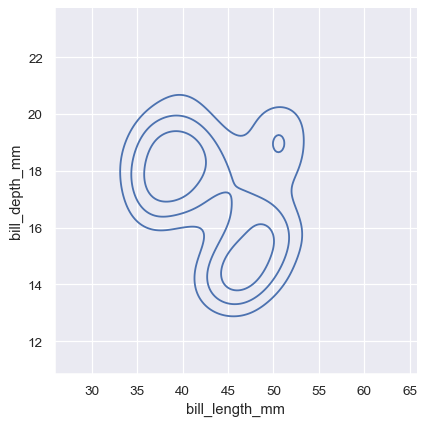
levelsパラメータは、より詳細な制御のために、値のリストも受け入れます。
sns.displot(penguins, x="bill_length_mm", y="bill_depth_mm", kind="kde", levels=[.01, .05, .1, .8])
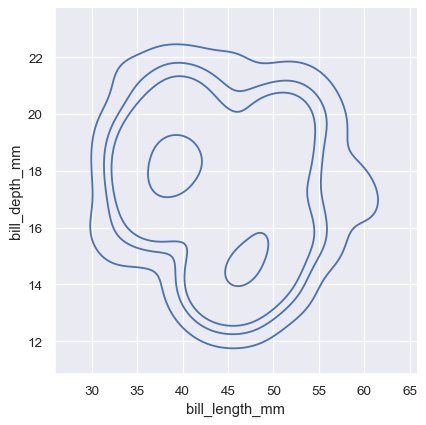
二変量ヒストグラムでは、一方または両方の変数を離散にすることができます。1つの離散変数と1つの連続変数をプロットすると、条件付き単変量分布を比較する別の方法が提供されます。
sns.displot(diamonds, x="price", y="clarity", log_scale=(True, False))
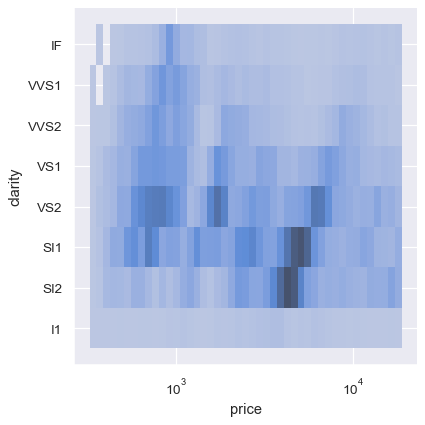
対照的に、2つの離散変数をプロットすると、観測値のクロス集計を簡単に表示できます。
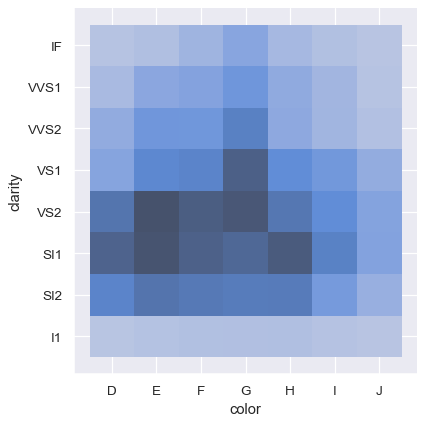
sns.displot(diamonds, x="color", y="clarity")
他の設定での分布の視覚化#
seabornの他のいくつかの図レベルのプロット関数は、histplot()関数とkdeplot()関数を使用します。
同時分布と周辺分布のプロット#
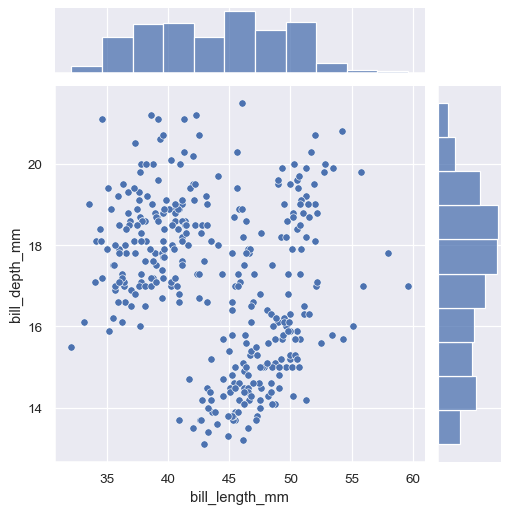
1つ目はjointplot()で、2変量の 관계 または分布プロットを、2つの変数の周辺分布で拡張します。デフォルトでは、jointplot()は、scatterplot()を使用して二変量分布を表し、histplot()を使用して周辺分布を表します。
sns.jointplot(data=penguins, x="bill_length_mm", y="bill_depth_mm")
displot()と同様に、jointplot()で別のkind="kde"を設定すると、同時プロットと周辺プロットの両方がkdeplot()を使用するように変更されます。
sns.jointplot(
data=penguins,
x="bill_length_mm", y="bill_depth_mm", hue="species",
kind="kde"
)
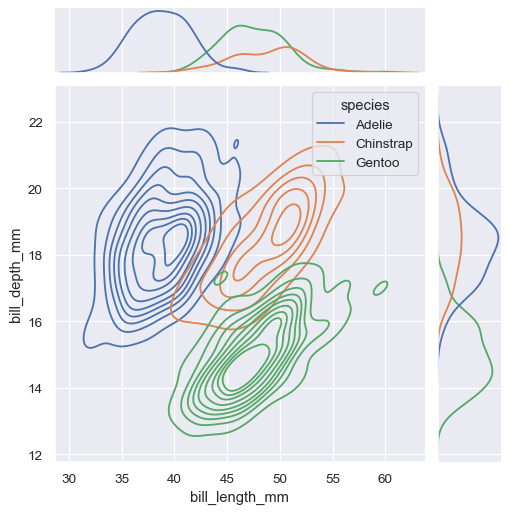
jointplot()は、JointGridクラスへの便利なインターフェースであり、直接使用するとより柔軟性が高まります。
g = sns.JointGrid(data=penguins, x="bill_length_mm", y="bill_depth_mm")
g.plot_joint(sns.histplot)
g.plot_marginals(sns.boxplot)
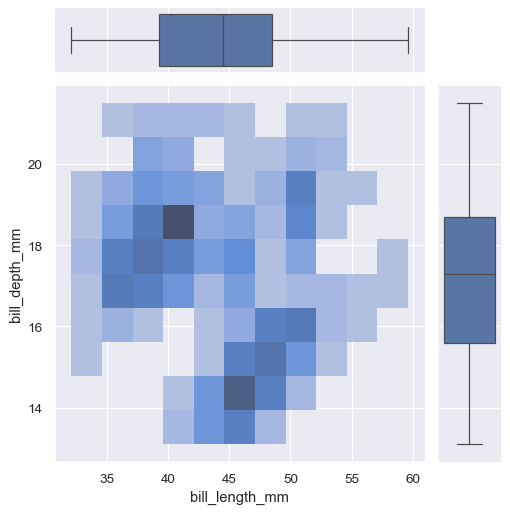
周辺分布を表示するそれほど邪魔にならない方法は、「ラグ」プロットを使用することです。これは、プロットの端に小さな目盛りを追加して、個々の観測値を表します。これはdisplot()に組み込まれています。
sns.displot(
penguins, x="bill_length_mm", y="bill_depth_mm",
kind="kde", rug=True
)
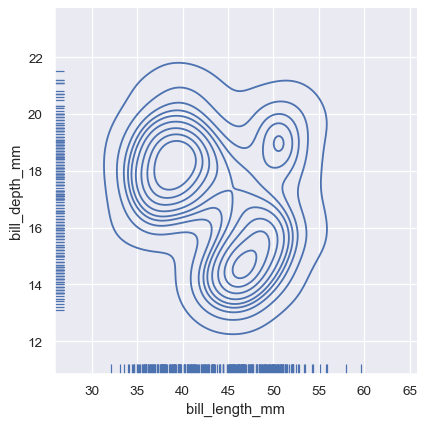
また、軸レベルのrugplot()関数は、他の種類のプロットの側にラグを追加するために使用できます。
sns.relplot(data=penguins, x="bill_length_mm", y="bill_depth_mm")
sns.rugplot(data=penguins, x="bill_length_mm", y="bill_depth_mm")
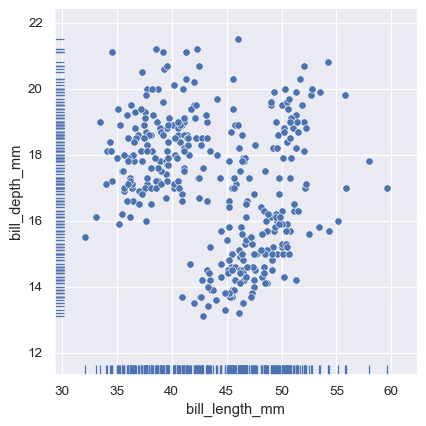
多数の分布のプロット#
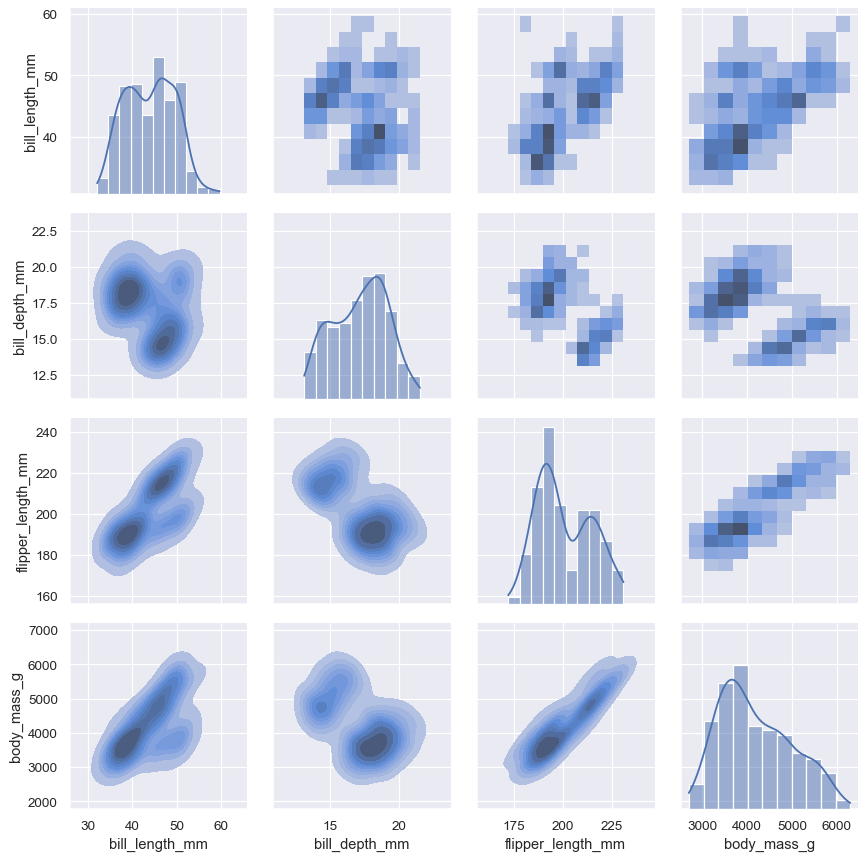
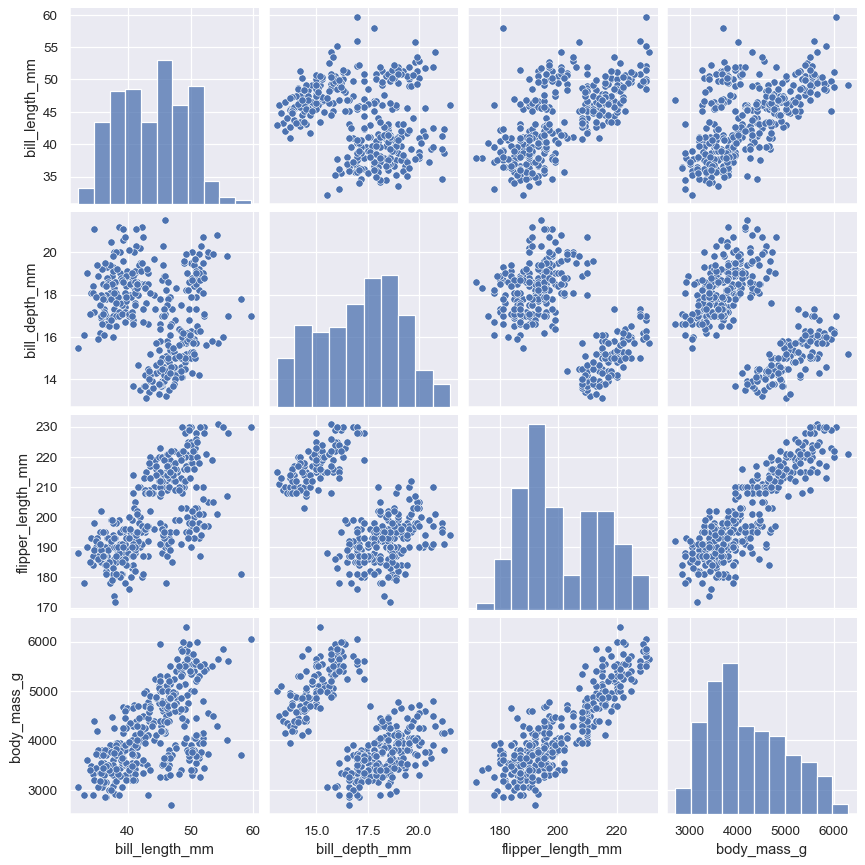
pairplot()関数は、同時分布と周辺分布の同様のブレンドを提供します。ただし、単一の 관계 に焦点を当てるのではなく、pairplot()は、「スモールマルチプル」アプローチを使用して、データセット内のすべての変数の単変量分布と、それらのすべてのペアワイズ 관계 を視覚化します。
sns.pairplot(penguins)
jointplot()/JointGridと同様に、基礎となるPairGridを直接使用すると、少しタイピングを増やすだけで、より柔軟性が高まります。
g = sns.PairGrid(penguins)
g.map_upper(sns.histplot)
g.map_lower(sns.kdeplot, fill=True)
g.map_diag(sns.histplot, kde=True)