回帰近似の推定#

多くのデータセットは複数の量的変数を含み、分析の目標はそれらの変数を互いに関連付けることです。2 つの変数の同時分布を示すことでこの目標を達成できる関数は、以前議論しました。ただし、ノイズのある 2 つの観測値セット間の単純な関係を推定するために統計モデルを使用すると非常に役立つ場合があります。この章で説明する関数は、線形回帰の一般的なフレームワークを通じてこれを行います。

Tukey の精神に沿って、Seaborn の回帰プロットは、探索的データ分析中にデータセットのパターンを強調する視覚的ガイドを追加することを主な目的としています。つまり、Seaborn は統計解析パッケージではありません。回帰モデルの近似に関連する定量的な測定値を取得するには、statsmodels を使用する必要があります。ただし、Seaborn の目標は、視覚化を通じてデータセットの探索を迅速かつ簡単に行うことです。統計表を通じてデータセットを探索するのと同じくらい重要（それ以上に重要）だからです。

線形回帰モデルの描画関数#

線形近似を視覚化するために使用できる 2 つの関数は、regplot() と lmplot() です。

最も単純な呼び出しでは、どちらの関数も 2 つの変数 x と y の散布図を描画してから、回帰モデル y ~ x を近似して生成された回帰線と、その回帰の 95% 信頼区間をプロットします。

tips = sns.load_dataset("tips")
sns.regplot(x="total_bill", y="tip", data=tips);
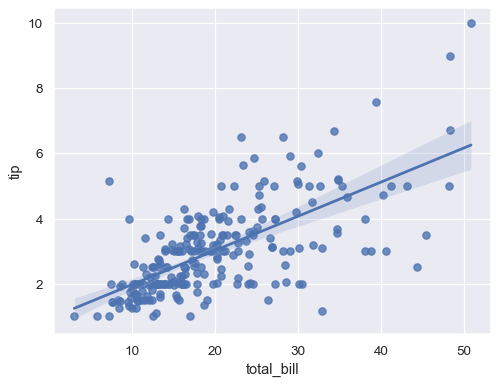
../_images/regression_4_0.png 
sns.lmplot(x="total_bill", y="tip", data=tips);
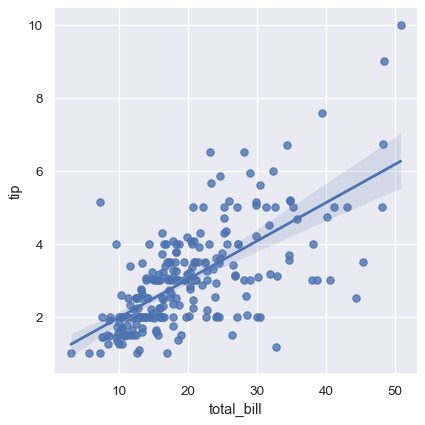
../_images/regression_5_0.png

これらの関数は同様のグラフを描画しますが、regplot() は軸レベル関数で、lmplot() は図形レベルの関数です。さらに、regplot() は、単純な numpy 配列、pandas.Series オブジェクト、または data に渡された pandas.DataFrame オブジェクト内の変数への参照など、さまざまな形式の x および y 変数を受け付けます。対照的に、lmplot()は必須パラメータとしてdata を持ち、x および y 変数は文字列として指定する必要があります。最後に、hue は lmplot() だけでパラメータとして使用できます。

ただし、コア機能はそれ以外は似ているため、このチュートリアルでは lmplot() に焦点を当てます。

変数のうち 1 つが離散値を取る場合は線形回帰を当てはめることができますが、この種のデータセットから作成される単純な散布図は最適ではありません。

sns.lmplot(x="size", y="tip", data=tips);
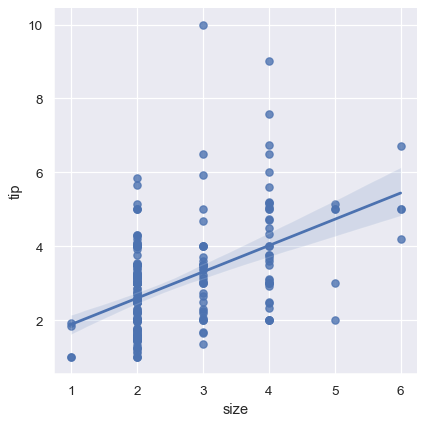
../_images/regression_7_0.png

1 つのオプションとして、離散値にランダムノイズ（「ジッター」）を追加して、それらの値の分布をより明確にすることができます。ジッターは散布図データにのみ適用され、それ自体が回帰線の適合に影響しないことに注意してください。

sns.lmplot(x="size", y="tip", data=tips, x_jitter=.05);
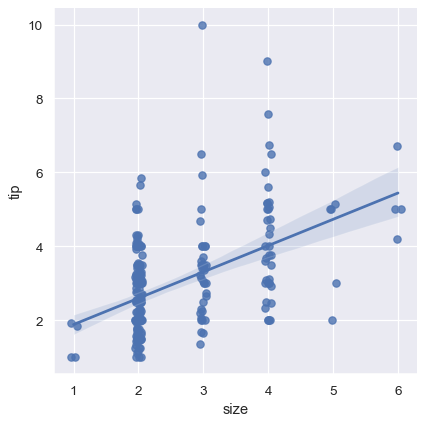
../_images/regression_9_0.png

2 つ目のオプションとして、各離散ビン内の観測値を折りたたんで、信頼区間と一緒に中心傾向の見積もりをプロットします。

sns.lmplot(x="size", y="tip", data=tips, x_estimator=np.mean);
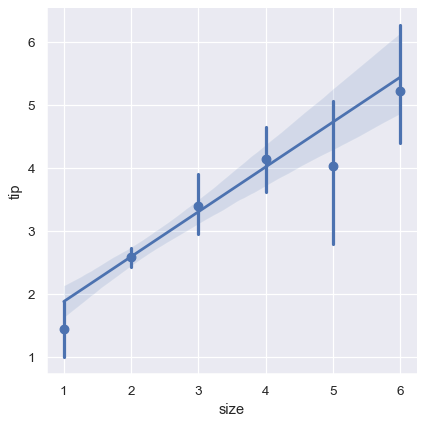
../_images/regression_11_0.png

さまざまな種類のモデルに適合#

上記で使用した単純な線形回帰モデルは非常に適合しやすいですが、一部のタイプのデータセットには適していません。Anscombe 4 重推定データセットには、単純な線形回帰が関係の同一の見積もりを提供するのに対し、単純な目視検査では明確に違いがあることが示されています。たとえば、最初のケースでは、線形回帰は良好なモデルです。

anscombe = sns.load_dataset("anscombe")

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'I'"),
           ci=None, scatter_kws={"s": 80});
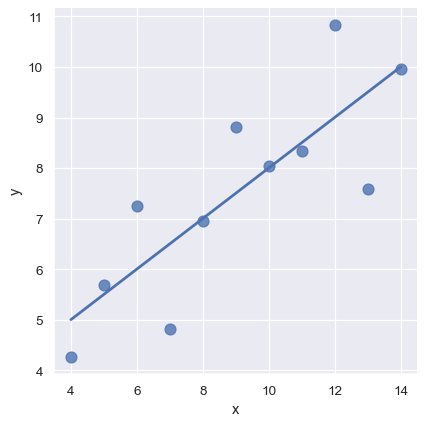
../_images/regression_14_0.png

2 番目のデータセットの線形関係は同じですが、グラフからはこれが適切なモデルではないことが明らかです。

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'II'"),
           ci=None, scatter_kws={"s": 80});
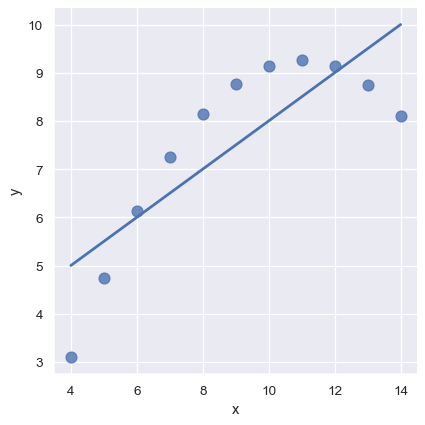
../_images/regression_16_0.png

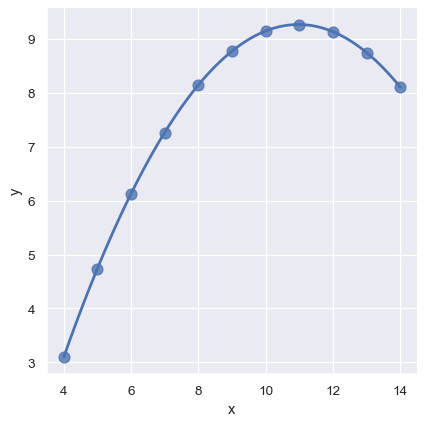
この種の高次の関係があると、lmplot() と regplot() は多項式回帰モデルを適合して、データセット内の単純な非線形傾向を調査できます。

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'II'"),
           order=2, ci=None, scatter_kws={"s": 80});
../_images/regression_18_0.png

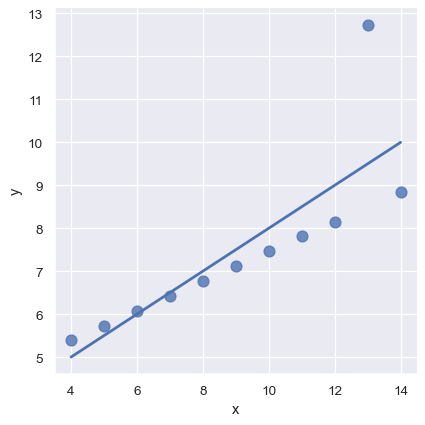
主な関係とは別の理由で逸脱する「外れ値」オブザベーションによって、異なる問題が提起されます

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'III'"),
           ci=None, scatter_kws={"s": 80});
../_images/regression_20_0.png

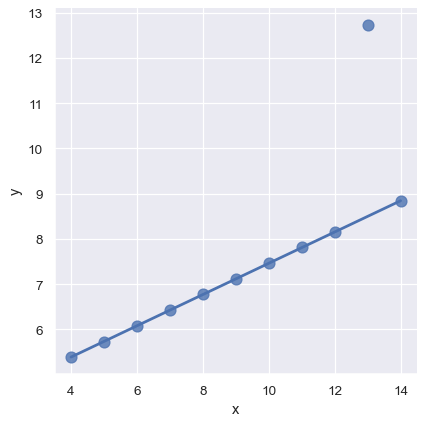
外れ値がある場合、比較的大きな残差を重み付けしてダウンさせるために異なる損失関数を使用する、頑健な回帰に適合させるのが有用となる場合があります

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'III'"),
           robust=True, ci=None, scatter_kws={"s": 80});
../_images/regression_22_0.png

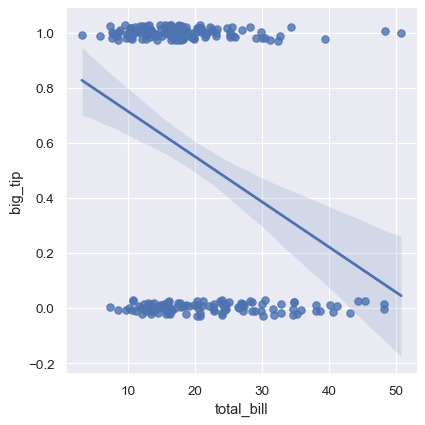
y変数がバイナリであると、単純線形回帰も機能しますが、あり得ない予測を行います

tips["big_tip"] = (tips.tip / tips.total_bill) > .15
sns.lmplot(x="total_bill", y="big_tip", data=tips,
           y_jitter=.03);
../_images/regression_24_0.png

この場合の解決策は、xの特定の値に対してy = 1の推定確率を示す回帰線を作成するロジスティック回帰に適合させることです

sns.lmplot(x="total_bill", y="big_tip", data=tips,
           logistic=True, y_jitter=.03);
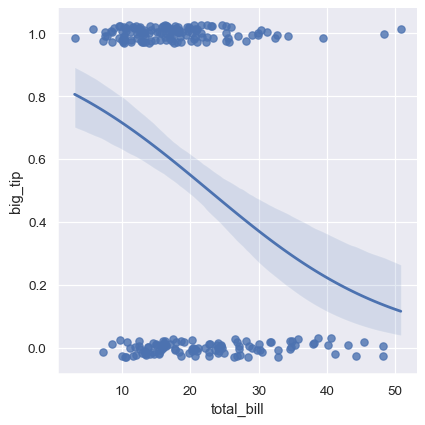
../_images/regression_26_0.png

ただし、ロジスティック回帰の推定値は、計算量がかなり多くなります（頑健な回帰でも同様です）。回帰線の周りの信頼区間はブートストラップ手順を使用して計算されるので、より高速な反復処理のために無効にしたくなる場合があります（ci=Noneを使用します）。

まったく異なるアプローチは、lowessスムージングを使用して非パラメトリック回帰に適合させることです。このアプローチは仮定が最も少ないですが、計算量が多いため、現在では信頼区間がまったく計算されていません

sns.lmplot(x="total_bill", y="tip", data=tips,
           lowess=True, line_kws={"color": "C1"});
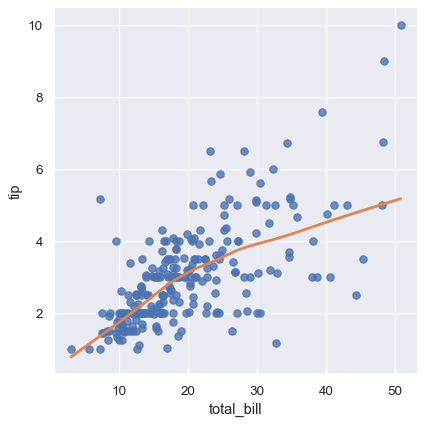
../_images/regression_28_0.png

residplot()関数は、単純回帰モデルがデータセットに適しているかどうかを確認するための便利なツールとなります。単純線形回帰に適合させ除去してから、各オブザベーションの残差値をプロットします。理想的には、これらの値はy = 0の周りにランダムに散らばっている必要があります

sns.residplot(x="x", y="y", data=anscombe.query("dataset == 'I'"),
              scatter_kws={"s": 80});
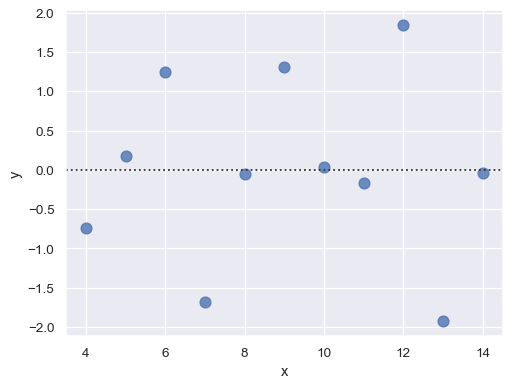
../_images/regression_30_0.png

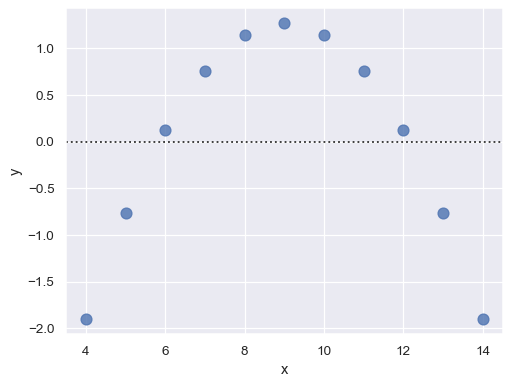
残差に構造がある場合は、単純線形回帰が適していないことが示されます

sns.residplot(x="x", y="y", data=anscombe.query("dataset == 'II'"),
              scatter_kws={"s": 80});
../_images/regression_32_0.png

他の変数による条件付け#

上記のプロットでは、一対の変数間の関係を調査するための多くの方法が示されています。しかし、往々にしてもっと興味深い質問は、「この2つの変数間の関係は、3番目の変数の関数としてどのように変化するか？」です。これがregplot()とlmplot()の主な違いが表れるところです。regplot()は常に単一の関係を示しますが、lmplot()はregplot()とFacetGridを組み合わせて、hueのマッピングまたはファセット化を使用して複数のフィットを表現します。

関係を分離する最良の方法は、両方のレベルを同じ軸上にプロットして、色を使用して区別することです

sns.lmplot(x="total_bill", y="tip", hue="smoker", data=tips);
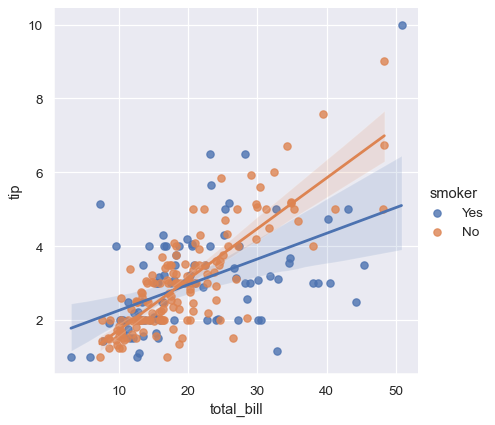
../_images/regression_34_0.png

relplot()とは異なり、散布図のスタイルプロパティに個別の変数をマップすることはできませんが、hue変数をマーカー形状で冗長にコード化できます

sns.lmplot(x="total_bill", y="tip", hue="smoker", data=tips,
           markers=["o", "x"], palette="Set1");
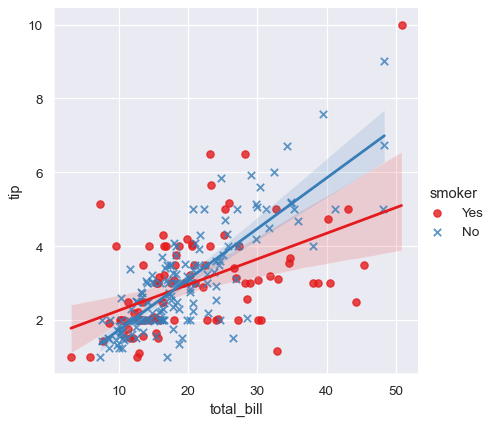
../_images/regression_36_0.png

別の変数を追加するには、複数の「ファセット」を描画して、変数の各レベルがグリッドの行または列に表れるようにできます

sns.lmplot(x="total_bill", y="tip", hue="smoker", col="time", data=tips);
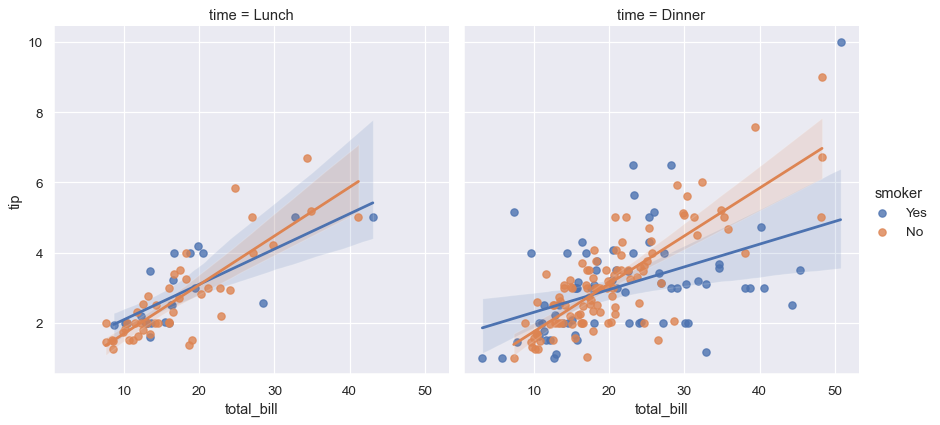
../_images/regression_38_0.png 
sns.lmplot(x="total_bill", y="tip", hue="smoker",
           col="time", row="sex", data=tips, height=3);
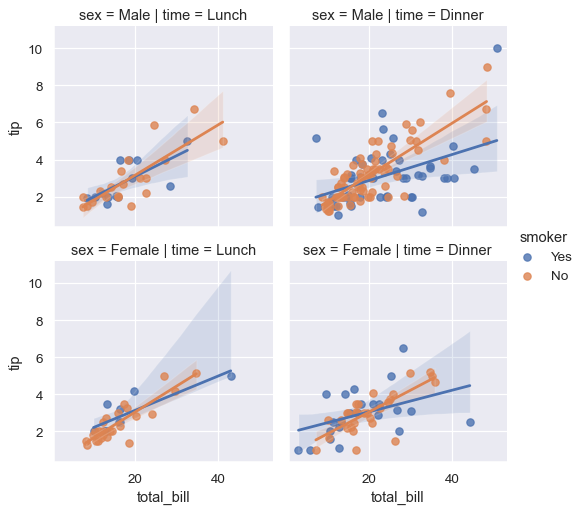
../_images/regression_39_0.png

他のコンテキストにおける回帰プロット#

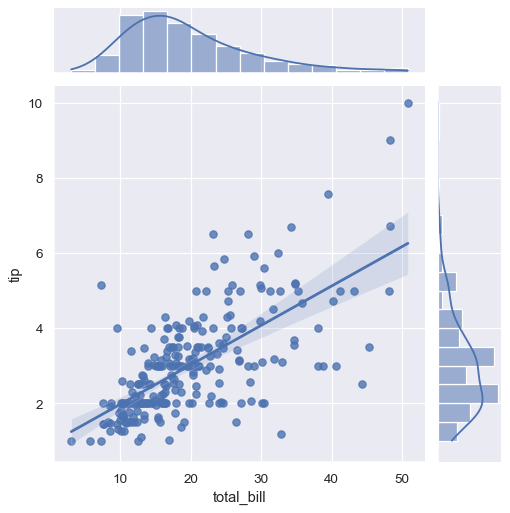
いくつかの他の seaborn 関数は、より大きく複雑なプロットのコンテキストで regplot() を使用しています。最初はその1つが jointplot() 関数で、分布チュートリアルで紹介しました。以前に説明したプロットスタイルに加えて、jointplot() は kind="reg"を渡すことで、ジョイント軸に線形回帰曲線を重ね書きする regplot() を使用できます

sns.jointplot(x="total_bill", y="tip", data=tips, kind="reg");
../_images/regression_41_0.png

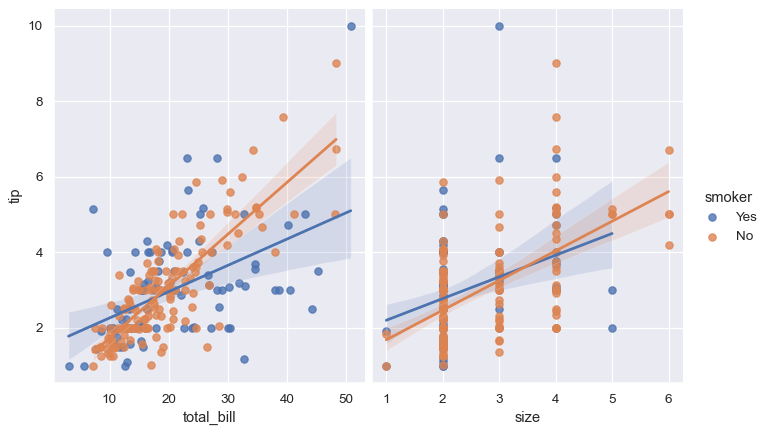
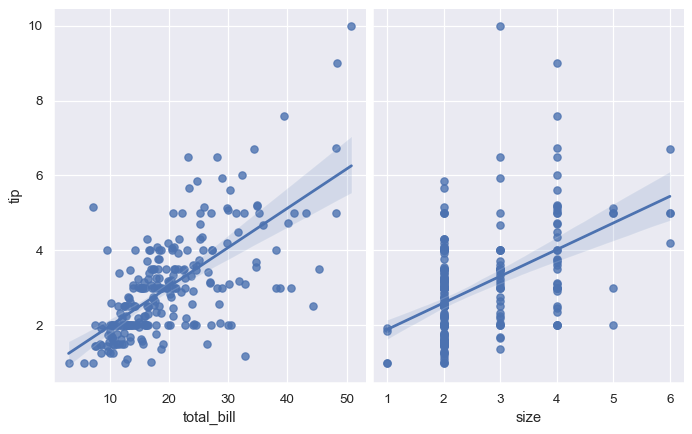
kind="reg" を使用して pairplot() 関数を使用すると regplot() と PairGrid が組み合わさり、データセット内の変数どうしの線形関係が示されます。この点が lmplot() とどのように異なるかに注意してください。以下の図で、2つの軸は3番目の変数の2つのレベルを条件とした同じ関係を示すわけではありません。むしろ、PairGrid() はデータセット内の変数のさまざまな組み合わせの複数の関係を示します

sns.pairplot(tips, x_vars=["total_bill", "size"], y_vars=["tip"],
             height=5, aspect=.8, kind="reg");
../_images/regression_43_0.png

追加のカテゴリ変数を条件とすることは、どちらの関数でも hue パラメータを使用して組み込まれています

sns.pairplot(tips, x_vars=["total_bill", "size"], y_vars=["tip"],
             hue="smoker", height=5, aspect=.8, kind="reg");
../_images/regression_45_0.png